WaterDistOpt

Multiobjective Optimization of Water Distribution Networks

Due to its practical importance and inherent complexity, the optimization of distribution networks for supplying drinking water has been the subject of extensive study for the past 30 years. The optimization is governed by sizing the pipes in the water distribution network (WDN). The pipe diameters are to be selected from a list of available commercial diameters, making WDN optimization a pure discrete optimization problem. Smaller diameters are cheaper, while larger diameters provide higher water pressure at the demand nodes. WDN optimization is an NP-hard problem with a search space that grows exponentially with the number of pipes in the network.

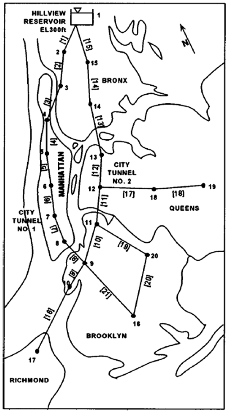Figure 1: Test problem New York City as presented in the 1969 study by Schaake and Lai.

Originally being a search for the least cost solution, subject to delivering pre-defined water demands to the consumer nodes at minimum required pressure, the optimization model has gradually changed to a multiobjective scheme including objectives for reliability under mechanical failure (e.g., pipe breakage) and hydraulic failure (e.g., increased demands). Evolutionary Algorithms (EAs) can directly deal with the discrete nature of WDN optimization and various Evolutionary Multiobjective Optimization Algorithms (EMOAs) are applied in this field, among which NSGA-II is highly popular. With respect to the common ZDT and DTLZ benchmarks, the Leiden developed SMS-EMOA outperformed NSGA-II. Motivated by these results, as a first study we compared the performance of SMS-EMOA to NSGA-II in the domain of WDN optimization using three classical benchmark problems.

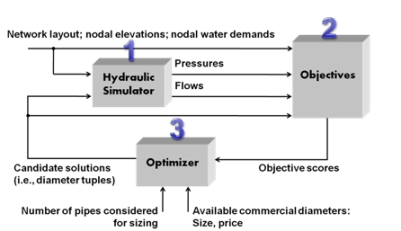Figure 2: The multiobjective optimization loop.

On these WDN benchmarks, SMS-EMOA consistently outperforms NSGA-II with respect to the applied multiobjective WDN model. The mean value of the attained hypervolume increased by 5% (Two Loop), 8% (New York City), and 200% (Hanoi). Based on the results we propose to use SMS-EMOA instead of NSGA-II for multiobjective WDN optimization. For future work we intend to do a performance comparison with native combinatorial optimizers such as Simulated Annealing, Tabu Search, and Ant Colony Optimization. Furthermore, we want to apply the developed methods to operational optimization of WDNs, involving the optimal scheduling of pumping facilities in order to minimize energy consumption.

Figure 3: The median attainment surfaces of the Pareto front approximations for test problem Hanoi over 30 runs per algorithm.